인덱스 트리
세그먼트 트리는 구현이 복잡하고 어렵다. 반면 인덱스 트리는 구현이 매우 간단하다
인덱스 트리를 활용하면 구간 합을 구하는 과정도 O(logN)의 시간 복잡도를 가진다.
인덱스 트리는 또한 세그먼트 트리에 비해서 메모리 효율성이 높다.
특정한 숫자 A의 마지막 비트를 구하고자 할 때 A&-A 연산을 통해서 구할 수 있다.
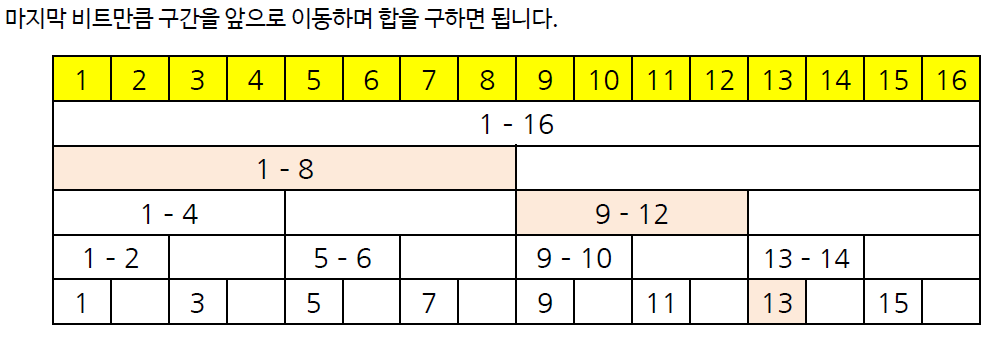
각 인덱스에 대하여 마지막 비트를 ‘내가 저장하고 있는 값들의 개수’로 표현한다.
ex)
16= 00010000(2) 16개
15= 00001111(2) 1개
14= 00001110(2) 2개
13= 00001101(2) 1
개
만일 13까지의 구간합을 구하고 싶다면 인덱스 [8] [12] [13] 의 값을 합하면 된다.
만일 5의 값을 수정하고 싶다면 인덱스 [5] [6] [8] [16] 의 값만 수정하면 된다.
#include<stdio.h>
#include<stdlib.h>
#define NUMBER 7
int tree[NUMBER];
int sum(int i){
int res=0;
while(i>0){
res+=tree[i];
i-=(i&-i);
}
return res;
}
void update(int i, int dif){
while(i<=NUMBER){
tree[i]+=dif;
i+=(i&-i);
}
}
int getSection(int start, int end){
return sum(end)-sum(start-1);
}
int main(void){
update(1, 7);
update(2, 1);
update(3, 9);
update(4, 5);
update(5, 6);
update(6, 4);
update(7,1);
printf("1부터 7까지의 구간 합: %d\n", getSection(1,7));
printf("인덱스 6의 원소를 +3만큼 수정\n");
update(6,3);
printf("4부터 7까지의 구간 합: %d\n", getSection(4, 7));
system("pause");
return 0;
}
인덱스 트리에서의 구간 합 계산 및 원소 수정 과정은 O(logN)의 시간 복잡도를 가진다.